Bạn đang tìm hiểu về công thức tính thể tích của các hình khối như hình nón, hình lặng trụ, hình tròn, hình chóp, hình vuông …
Hôm nay chúng tôi xin gửi đến các bạn toàn bộ các công thức tính thể tích của các hình đếp áp dụng cho việc học của các bạn được tốt hơn.
- Nguyên hàm là gì ? Công thức tính nguyên hàm.
- Tích có hướng là gì ?
- Đạo Hàm là gì ?
Định nghĩa về thể tích
Thể tích, hay dung tích, của một vật là lượng không gian mà vật ấy chiếm. Thể tích có đơn vị đo là lập phương của khoảng cách (khoảng cách mũ 3).
Trong Hệ đo lường quốc tế, do đơn vị đo của khoảng cách là mét, đơn vị đo của thể tích là mét khối, ký hiệu là m³
Đơn vị tính thể tích
Bất kỳ đơn vị độ dài nào cũng có đơn vị thể tích tương ứng: thể tích của khối lập phương có các cạnh có chiều dài nhất định. Ví dụ, một xen-ti-mét khối (cm3) là thể tích của khối lập phương có cạnh là một xentimét (1 cm).
Trong Hệ đo lường quốc tế (SI), đơn vị tiêu chuẩn của thể tích là mét khối (m3). Hệ mét cũng bao gồm đơn vị lít (litre) (kí hiệu: L) như một đơn vị của thể tích, trong đó một lít là thể tích của khối lập phương 1 dm. Như vậy
1 lít = (1 dm)3 = 1000 cm3 = 0.001 m3
vậy
1 m3 = 1000 lít.
Một lượng nhỏ chất lỏng thường được đo bằng đơn vị mililít (ml) (Tiếng Anh: mililitre)
1 ml = 0.001 lít = 1 xentimét khối.
Cũng như vậy, một lượng lớn chất lỏng thường được đo bằng đơn vị mêgalít (Tiếng Anh: megalitre)
1 000 000 lít = 1000 mét khối = 1 mêgalít (Ml). (Lưu ý Megalitre được kí hiệu là Ml, không phải ml như mililitre)
Công thúc tính thể tích hình khối nón
Với: πr2h/3 với r là bán kính đáy, h là chiều cao.
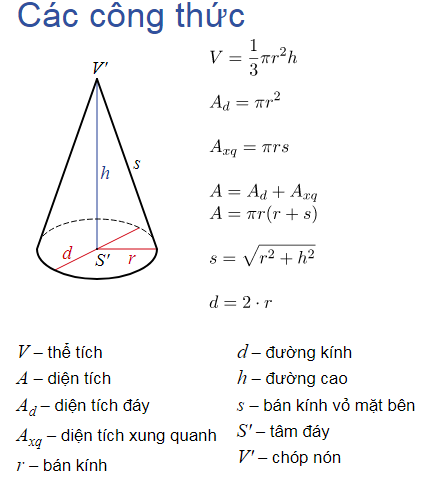
Công thức tính thể tích hình hộp chữ nhật
Với : a x b x c với a là chiều dài,b là chiều rộng,c là chiều cao của hình hộp chữ nhật.

Công thúc tính thể tích hình trụ tròn xoay
Với : πr2h với r là bán kính đáy, h là chiều cao.
Công thức tính thể tích hình chóp
Với : πr2h với rSh/3 với S là diện tích đáy, h là chiều cao. là bán kính đáy, h là chiều cao.
Công thức tính thể tích hình lăng trụ.
Trong hình học, hình lăng trụ là một đa diện có hai mặt đáy là các đa giác tương đẳng và những mặt còn lại là các hình bình hành.[1] Mọi tiết diện song song với hai đáy đều là các đa giác tương đẳng với hai đáy.

Với những chia sẻ kiến thức nhỏ bé ở bài viết này chúng tôi mong sẽ giúp được các bạn đôi chút kiến thức về công thức tính thể tích khối chóp, hình nón, hình vuông, hình tròn xoay, hình lăng trụ …
