Định nghĩa

Số Phức là gì ?
Số phức là số có thể viết dưới dạng trong đó a và b là các số thực là đơn vị ảo, với {2}=-1} hay = -1}.
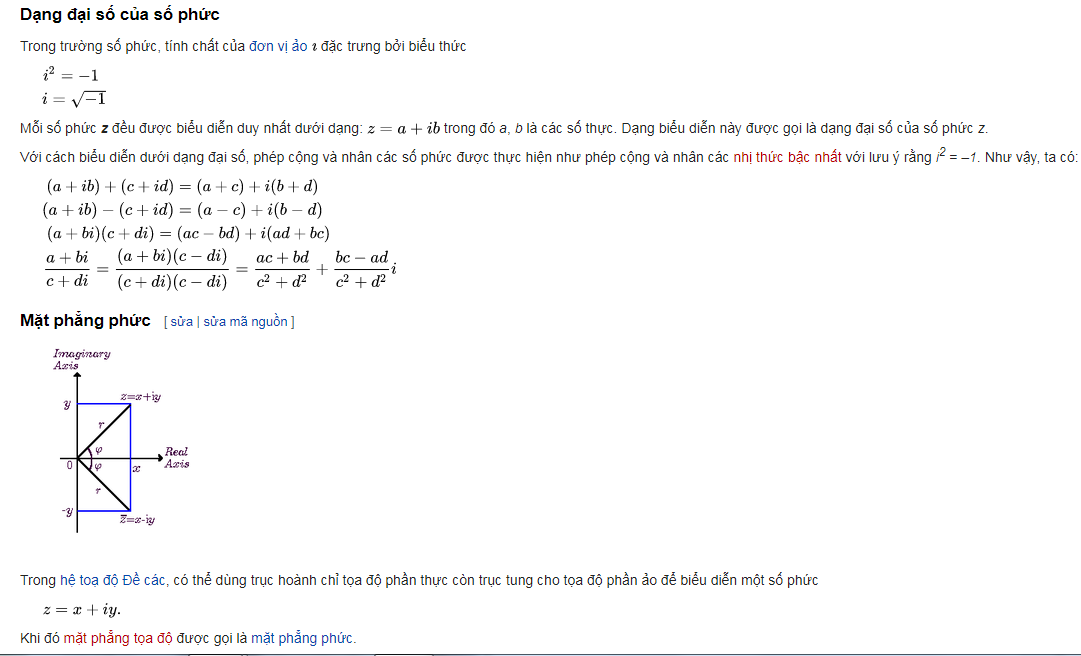
Trong biểu thức này, số a gọi là phần thực, b gọi là phần ảo của số phức. Số phức có thể được biểu diễn trên mặt phẳng phức với trục hoành là trục thực và trục tung là trục ảo, do đó một số phức a+b được xác định bằng một điểm có tọa độ (a,b).
Một số phức nếu có phần thực bằng không thì gọi là số thuần ảo, nếu có phần ảo bằng không thì trở thành số thực. Việc mở rộng trường số phức để giải những bài toán mà không thể giải trong trường số thực.
Số phức z có dạng z = a + bi với a, b là số thực và i là đơn vị ảo (i2 = -1).
– a là phần thực, b là phần ảo, C là tập hợp số phức và R ⊂ C.

– Biểu diễn hình học: Trong mpOxy, mỗi điểm M(a ; b) hay vectơ = (a ; b) biểu diễn số phức z = a + bi,
khi đó Ox là trục thực, Oy là trục ảo và (Oxy) là mặt phẳng phức.

– Cho z = a + bi và z’ = a’ + b’i. Khi đó
Số phức có dạng a+bia+bi
- a, b là các số thực
- i là đơn vị ảo
Với i2=−1i2=−1
Nếu ta lấy phần thực của số phức thì đó là a. Nếu ta lấy phần ảo của số phức thì đó là b.
Ví dụ số phức:
- 2 + 3i –> phần thực: 2, phần ảo: 3
- 4 – 2i
- -5 + i
- -6 – 4i
- 1.2 + 5.1i
- 4.4 = 4.4 + 0i –> trong trường hợp này, hệ số b của đơn vị ảo bằng 0
Vậy ta có thể thấy rằng số phức là trường hợp tổng quát hơn của số thực. Số thực là 1 trường hợp cụ thể của số phức (khi b = 0). Để dễ hình dung nhất về số phức. Ta tiến hành so sánh và minh họa cụ thể chúng trong không gian 2 chiều trong phần tiếp theo.
Tổng quan về Số Phức

Khái niệm


Xem ví dụ:
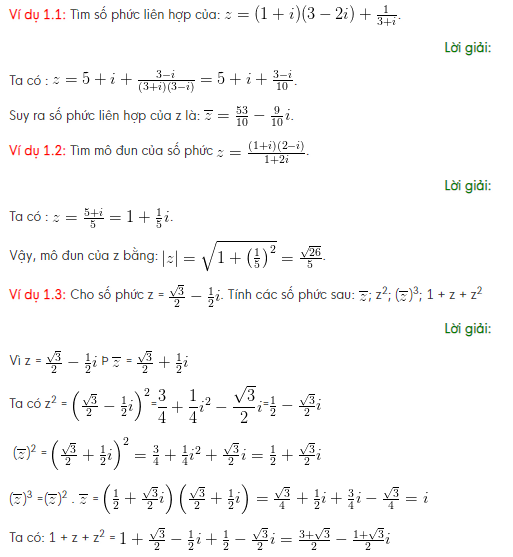

Với những chia sẻ về số phúc của chúng tôi mong các bạn trẻ sẽ có thêm được chút kiến thức về số phúc. Chúc các bạn học thật giỏi.