Công thức đạo hàm logarit và mũ có bài tập minh họa có lời giải

Trong bài viết dưới đây, chúng tôi sẽ chia sẻ công thức đạo hàm logarit và mũ giúp các bạn ôn lại kiến thức để vận dụng các công thức đạo hàm để giải các bài tập trong sách giáo khoa và các bài tập nâng cao nhé.

Công thức đạo hàm logarit

Cho hàm số y = log_ax. Khi đó đạo hàm của hàm số trên là:

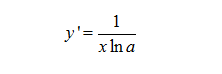
Trường hợp tổng quát hơn, cho hàm số y = log_au(x). Đạo hàm là:

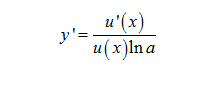
Bảng công thức đạo hàm logarit

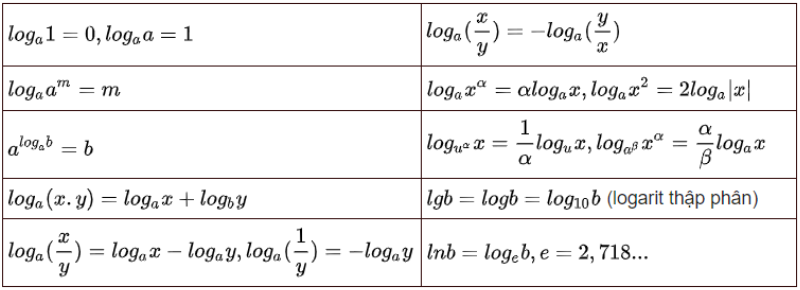
Ngoài ra, các bạn muốn tìm hiểu rõ hơn về định nghĩa, công thức đạo hàm và bảng đạo hàm cơ bản đến nâng cao chi tiết tại đây.

Công thức đạo hàm mũ

Cho hàm số y = a^x. Đạo hàm của hàm số là: y’ = a^x lna

Trường hợp tổng quát hơn, y = a^u(x). Ta có: y’ = u'(x)a^u(x)lna

Bảng công thức đạo hàm mũ

Các dạng bài tập về công thức đạo hàm logarit và mũ

Ví dụ 1: Tính đạo hàm của hàm số y=log₂(x²+x+1).

Giải

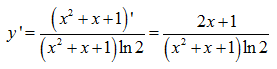
Ví dụ 2: Tính đạo hàm của các hàm số sau:

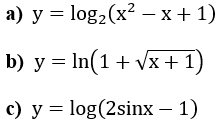
Lời giải:

Ví dụ 3: Tính đạo hàm của các hàm số sau:

Lời giải:

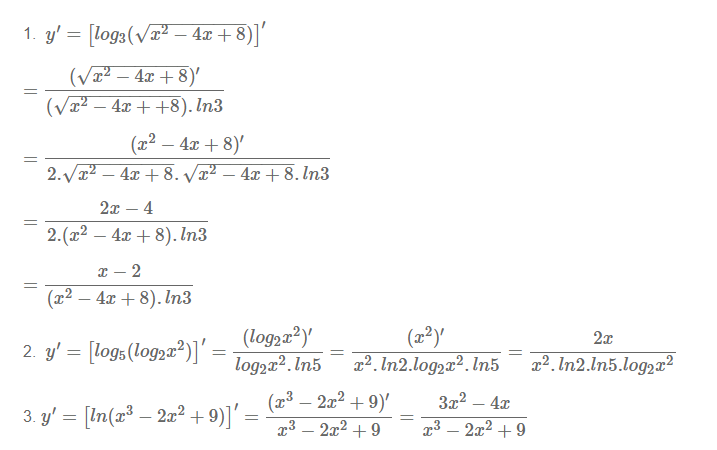
Hy vọng với những kiến thức về bảng công thức đạo hàm mũ và logarit mà chúng tôi vừa phân tích chi tiết phía trên có thể giúp các bạn ghi nhớ được các công thức nhanh chóng nhé